📚 [비전] ResNet 논문 리뷰 및 요약
📌 개요
✔ ResNet 논문 키포인트
1. Shortcut Connection을 통한 Residual Learning을 고안하여 네트워크의 depth를 늘릴 때의 degradation 문제를 해결.
2. ResNet은 152개 layers로 depth를 크게 늘리면서 이전의 VGGNet에 비해 8배 더 깊은 네트워크 구조를 만들어냄.
3. ILSVRC 2015에서 1위를 차지하였으며 top-5 error rate 3.57% 달성하며 인간보다 더 낮은 오류를 보여줌.
📌 Degradation 문제
✔ 심층 신경망의 깊이를 늘릴 때 degradation 문제
1. 심층 신경망의 깊이를 늘릴 때 vanishing/exploding gradient 문제 뿐만 아니라 degradation 문제가 발생함.
2. degradation은 overfitting으로 발생하는 것이 아님. 아래의 Figure 1 그래프를 보면 20-layer와 56-layer plain 네트워크를 CIFAR-10 데이터에 대해 실험했을 때 56-layer 네트워크에서 20-layer 네트워크보다 training error와 test error가 더 높다는것을 확인할 수 있다. 즉, 심층 신경망의 깊이를 늘렸을 때 만약 training error가 낮아지고 test error가 높아졌다면 그건 overfitting 문제겠지만, training과 test error 모두 높아졌기 때문에 이는 레이어를 깊게 쌓을수록 성능이 저하되는 degradation 문제이다.

📌 Deep Residual Learning
✔ Residual Learning
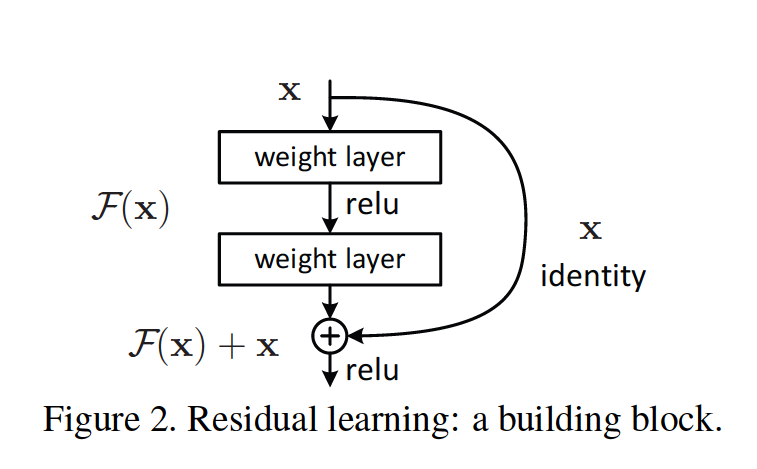
1. 이 논문에서는 심층 신경망의 depth를 늘릴 때 발생하는 degradation 문제를 해결하기 위해 Deep Residual Learning Framework를 제안하였다.
2. 네트워크의 a few stacked non-linear layers의 입력이 $x$일 때 이 레이어들이 최적화할 underlying mapping을 $H(x)$ 라고 하자. 네트워크의 a few stacked non-linear layers에서 입력 $x$를 처리하여 이전 레이어의 학습에서와 달라지는 부분을 $F(x)$라고 할 때, $H(x) = F(x) + x$ 로 표현할 수 있다. 여기서 원래의 $H(x)$를 최적화하는 대신, residual mapping인 $F(x)$를 최적화하는 것이 더 쉽다고 가정할 수 있다. 극단적인 예로, 네트워크의 a few stacked non-linear layers에 입력으로 들어온 $x$가 최적이었다고 해보자. 그러면 이 레이어들이 $H(x) = x$로 최적화하는 것보다도, $x$에 추가적으로 학습하는 부분인 residual을 0으로 만드는 것이 훨씬 쉽다.
3. 즉, 기존에는 레이어들이 desired underlying mapping에 최적화하는 것이 목적이었다면, 이 논문에서 새롭게 정의된 구조에서는 residual mapping에 최적화하는 것이 목적이 된다.
✔ Residual Learning을 실현하는 Shortcut Connection 구조
1. 이 논문에서는 네트워크의 every few stacked layers에 residual learning을 적용하게 되는데 이렇게 적용된 각각의 building block은 다음과 같은 수식으로 표현할 수 있다.
$y = F(x, \left\{W_{i}\right\}) + x $
이 때, $x$와 $y$는 개별 residual block에 포함된 레이어들의 입력과 출력 벡터를 의미하며, $F(x, \left\{W_{i}\right\})$는 학습할 residual mapping을 의미한다.
2. $F + x$ 연산은 shortcut connection 구조를 통해 이루어지며, element-wise 합이다.
3. 이러한 shortcut connection 구조는 추가적인 파라미터나 계산 복잡도를 요구하지 않기 때문에 효율적이다.
4. 만약 $x$와 $F$의 차원이 변경되는 구간에서는, 차원이 늘어난만큼 zero padding을 해주거나, linear projection으로 차원 변경을 수행할 수 있다.
📌 ResNet의 구조와 성능 실험
✔ Plain 네트워크(34 layers)와 Residual 네트워크(34 layers) 구조 비교

1. VGG-19는 참고용으로, plain 네트워크를 디자인할 때 VGGNet 구조를 참고하였다고 함.
2. convolution layers는 모두 3x3 filter size를 사용.
3. convolution layers의 stride를 2로 하여 downsampling 수행.
4. 네트워크의 Feature Extractor에서 Classifier의 사이에서는 global average pooling을 진행하고 Classifier 부분에서는 1000개 라벨로 분류하는 FC layer에 softmax 함수 적용.
5. plain 네트워크와 residual 네트워크의 전체적인 디자인은 동일하되, residual 네트워크에는 shortcut connections을 통한 residual learning을 구현하여 plain 네트워크와의 비교 실험 진행.
✔ Plain 네트워크(34 layers)와 Residual 네트워크(34 layers) 비교 실험
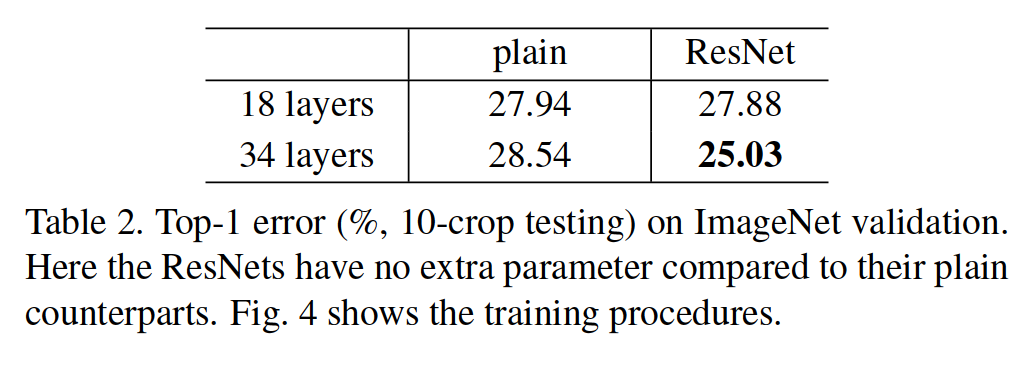
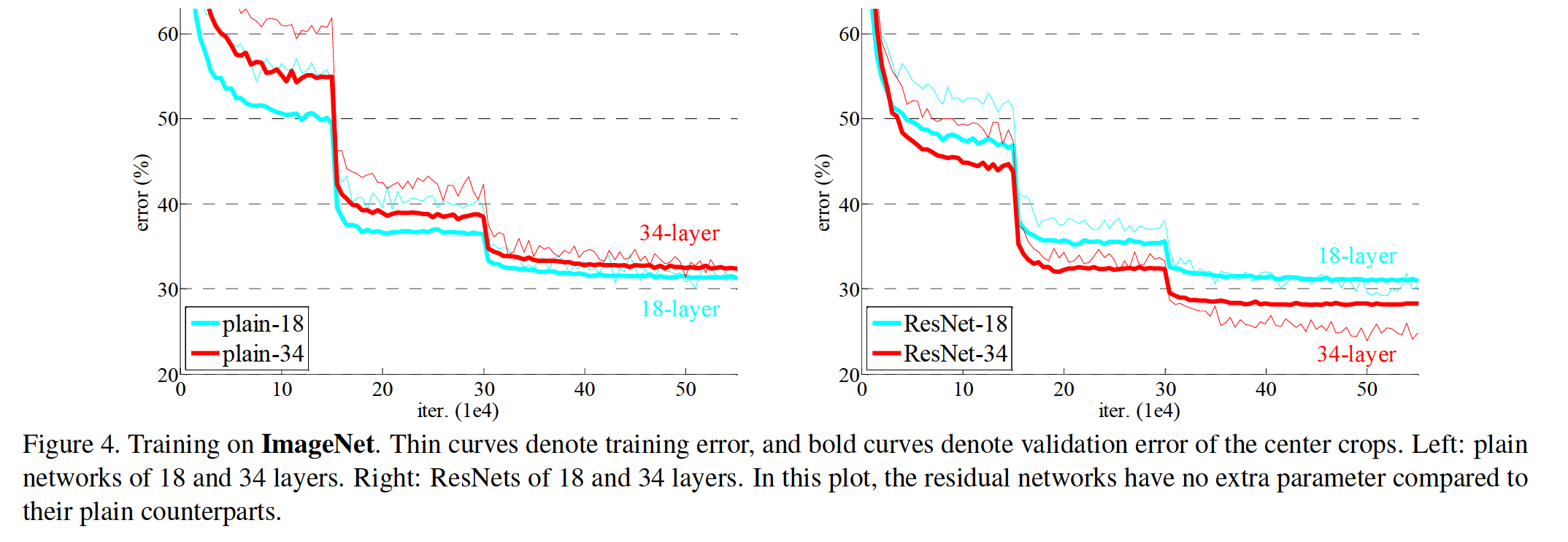
1. ImageNet 데이터에 대하여 plain 네트워크와 residual 네트워크를 각각 18 layers, 34 layers로 실험한 결과는 다음 표와 그래프를 통해 확인할 수 있다.
2. Table 2를 보면 18 layers일 때 top-1 error rate는 plain 네트워크에서 27.94%이고 residual 네트워크에서는 27.88%로 residual 네트워크의 성능이 더 좋다. 특히 이 성능 차이는 네트워크의 depth를 늘렸을 때 현저히 드러나는데, 34 layers일 때 top-1 error rate는 plain 네트워크에서 28.54%이고 residual 네트워크에서 25.03%이다. ResNet에서는 depth를 늘렸을 때 degradation 문제가 해결되었음을 확인할 수 있다.
3. Figure 4를 보면 ResNet은 plain 네트워크보다 빠르게 최적화되는 것도 확인할 수 있다.
✔ ResNet의 depth별 구조 및 parameter 개수

논문 링크 : https://arxiv.org/pdf/1512.03385.pdf



