📚 [비전] EfficientNet 논문 리뷰 및 요약
📌 개요
✔ EffiicentNet 논문 키포인트
1. Compound Scaling 방법을 통해 depth, width, resolution 3가지 요소를 복합적으로 증가시켜 모델 성능 향상.
2. Neural Architecture Search 방법을 통해 베이스라인 모델 구조를 효율적으로 디자인.
3. 높은 성능, 적은 수의 파라미터, 적은 수의 FLOPS를 가진 효율적인 모델 구조로 SOTA 달성.
📌 Model Scaling
✔ CNN의 성능을 높이기 위해서 Model Scaling을 적용할 3가지 요소
1. Depth(레이어의 개수) : 네트워크를 깊게 쌓으면 더 다양하고 복잡한 features를 파악할 수 있고 새로운 task에 대해서도 일반화를 잘 할 수 있다.
2. Width(채널 개수) : 네트워크의 채널 개수를 많이 설정하면 정교한 features를 파악할 수 있고 학습도 좀 더 쉽게 이루어질 수 있다.
3. Resolution(이미지 크기) : 이미지 크기가 크면 좀 더 정교한 패턴을 파악할 수 있다.
✔ 기존의 Model Scaling과 이 논문에서 제안하는 Compound Scaling 비교

1. 기존의 Model Scaling은 depth(레이어의 개수), width(채널 개수), resolution(이미지의 크기) 3가지 요소 중 한가지만 증가시키는 방식이었다.
2. 이 논문에서 제안하는 Compound Scaling은 depth, width, resolution 3가지 요소를 균형있게 증가시키는 방식이다. 이와 관련하여 직관적인 예를 들어보자. 입력되는 이미지의 크기가 커지면(higher resolution) receptive field가 커지므로 네트워크에서 더 많은 레이어가 필요할 것이고(deeper) 이미지의 정교한 패턴을 포착하기 위해 더 많은 채널이 필요할 것(wider)이다.
✔ 기존의 Model Scaling 방식의 한계

기존의 방식대로 width scaling, depth scaling, resolution scaling을 각각 적용할 경우에는 성능 향상이 되더라도 빠르게 둔화된다. 즉, 각각의 요소를 개별적으로 늘리는 것만으로는 한계가 있다.
참고로 기존에는 한가지 요소만 scaling했던 이유는, depth, width, resolution 최적값이 상호 의존적이라는 점, 리소스 제약이 달라지면 depth, width, resolution 최적값도 달라진다는 점으로 인해 세가지 요소를 한꺼번에 증가시키는 것이 어려웠기 때문이다.
✔ Compound Scaling의 필요성
아래의 Figure 4를 보면 서로 다른 depth와 resolution 조건 하에서 width scaling을 적용할 때의 성능 실험을 한 결과가 나와있다. 동일 FLOPS에서 deeper and higher resolution인 네트워크일수록 width scaling한 경우 성능이 더 좋다는 사실을 확인할 수 있다. 즉 모델의 성능과 효율성을 개선하려면 depth, width, resolution을 복합적으로 증가시키는 것이 중요하다.

📌 Compound Scaling
✔ Compound Scaling
1. 기존에도 depth, width, resolution을 함께 늘려보려는 시도가 있었으나 정형화된 방법을 사용하는 것이 아니라 임의로 직접 튜닝하는 방식에 가까웠다.
2. 이 논문에서는 compound coefficient를 사용하여 가용 리소스에 따라 depth, width, resolution을 조화롭게 증가시키는 방식을 사용한다.
✔ Compound Scaling 방법

1. compound coefficient $\Phi$는 model scaling에 추가적인 리소스를 얼마나 사용할 것인지에 따라 사용자가 그 값을 정할 수 있다.
2. $\alpha, \beta, \gamma$는 각각 depth, width, resolution에 가용 리소스를 얼마나 할당할 수 있는지를 의미하며, grid search를 통해 찾은 상수이다.
3. CNN에서 depth가 2배가 되면 convolution 연산의 FLOPS가 2배가 되지만, width나 resolution은 2배가 되면 convolution 연산의 FLOPS가 4배가 된다. 따라서 네트워크를 scaling up할 때 total FLOPS가 $2^{\Phi}$을 넘지 않도록 하려면 $\alpha\beta^{2}\gamma^{2}\approx2$ 제약을 만족해야 한다.
참고로 FLOPS은 일반적으로 컴퓨터에서 1초 동안의 부동소수점 연산 횟수를 말하지만 딥러닝에서는 모델의 연산 횟수를 의미하기 때문에, FLOPS가 커지면 모델의 연산량이 커지고 동작시간이 길어진다.
c.f. 딥러닝에서의 FLOPS의 의미 : https://stackoverflow.com/questions/58498651/what-is-flops-in-field-of-deep-learning
📌 Neural Architecture Search
✔ Neural Architecture Search
1. Model Scaling을 적용할 때 그 베이스라인 네트워크가 무엇인가에 따라 효과가 달라지므로 더 나은 베이스라인 구조를 찾기 위해 Neural Architecture Search 진행. 이는 기존의 MnasNet 논문에서 사용한 방식을 따름.
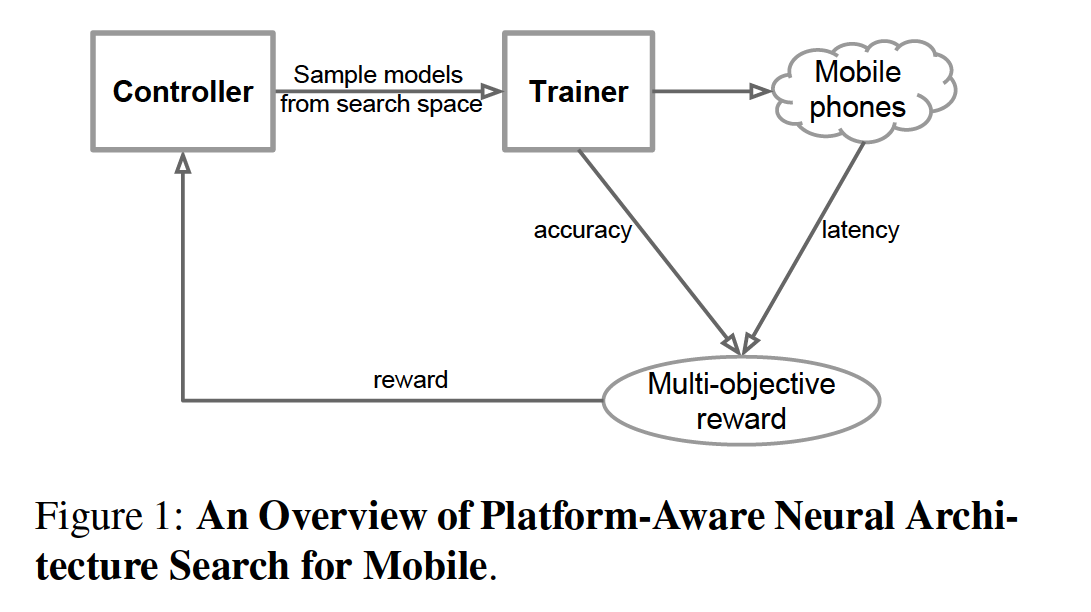
2. accuracy와 FLOPS를 모두 최적화하는 구조를 찾기 위해서 $ACC(m) \times [FLOPS(m)/T]^{w}$ 산식을 만족하는 네트워크를 서치하여 베이스라인으로 EfficientNet-B0을 도출.

📌 EfficientNet의 구조
✔ Compound Scaling 적용
1. 베이스라인 모델 EfficientNet-B0 기준으로 $\alpha, \beta, \gamma$의 최적값을 도출 : 2배의 리소스가 가능하다는 가정 하에, 일단 $\Phi=1$로 설정하고 $\alpha\beta^{2}\gamma^{2}\approx2$ 제약 조건 하에서 $\alpha, \beta, \gamma$에 grid search를 적용해서 $\alpha=1.2, \beta=1.1, \gamma=1.15$ 라는 최적값을 구함.
2. $\alpha, \beta, \gamma$를 고정한 상태에서 $\Phi$를 변화시키면서 Compound Scaling : $\alpha, \beta, \gamma$는 베이스라인 모델 EfficientNet-B0에서 찾은 최적값으로 고정하되, compound coefficient $\Phi$을 다르게 하여 모델을 scale up하여 EfficientNet-B1 ~ B7까지 도출.
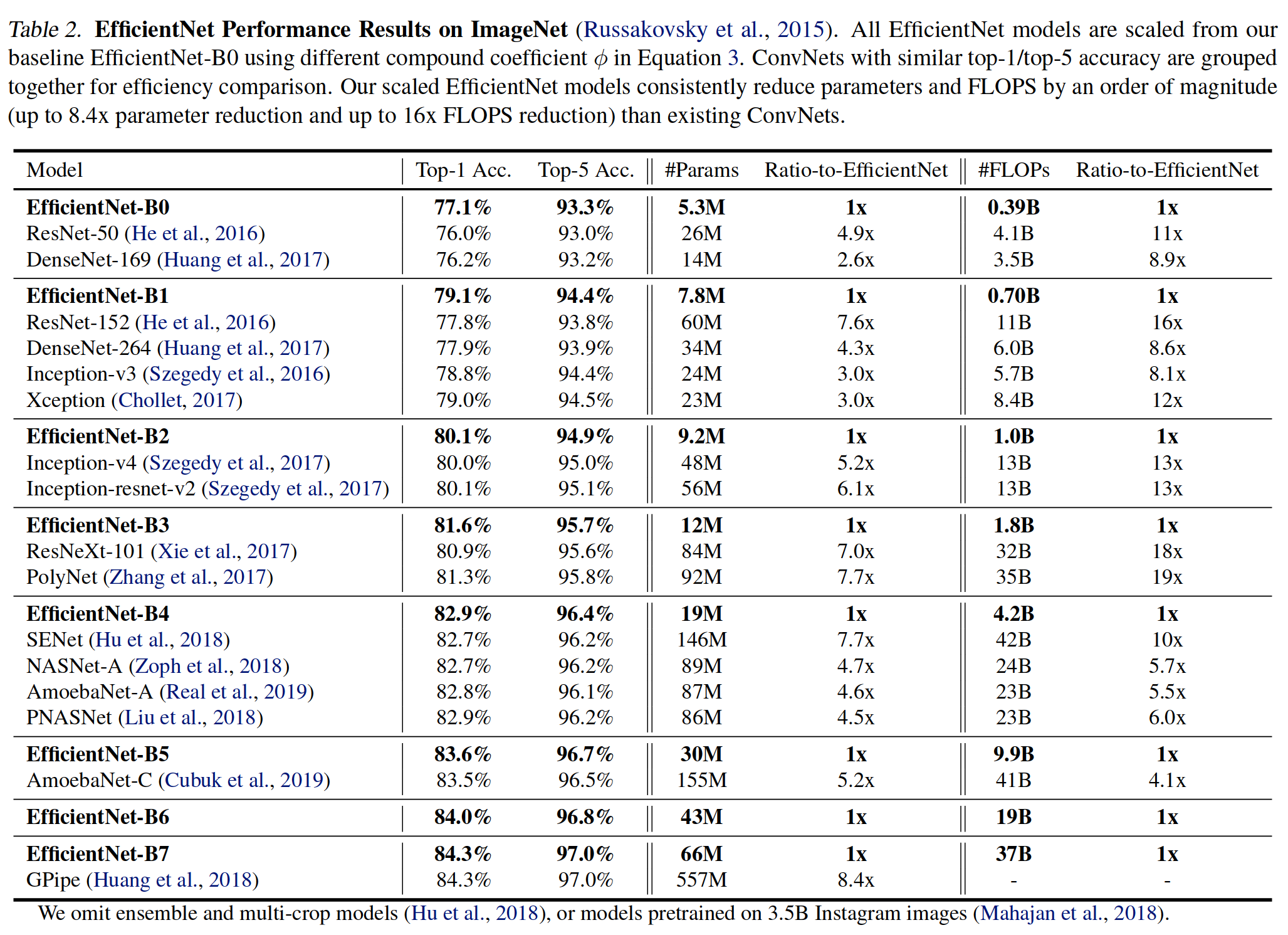
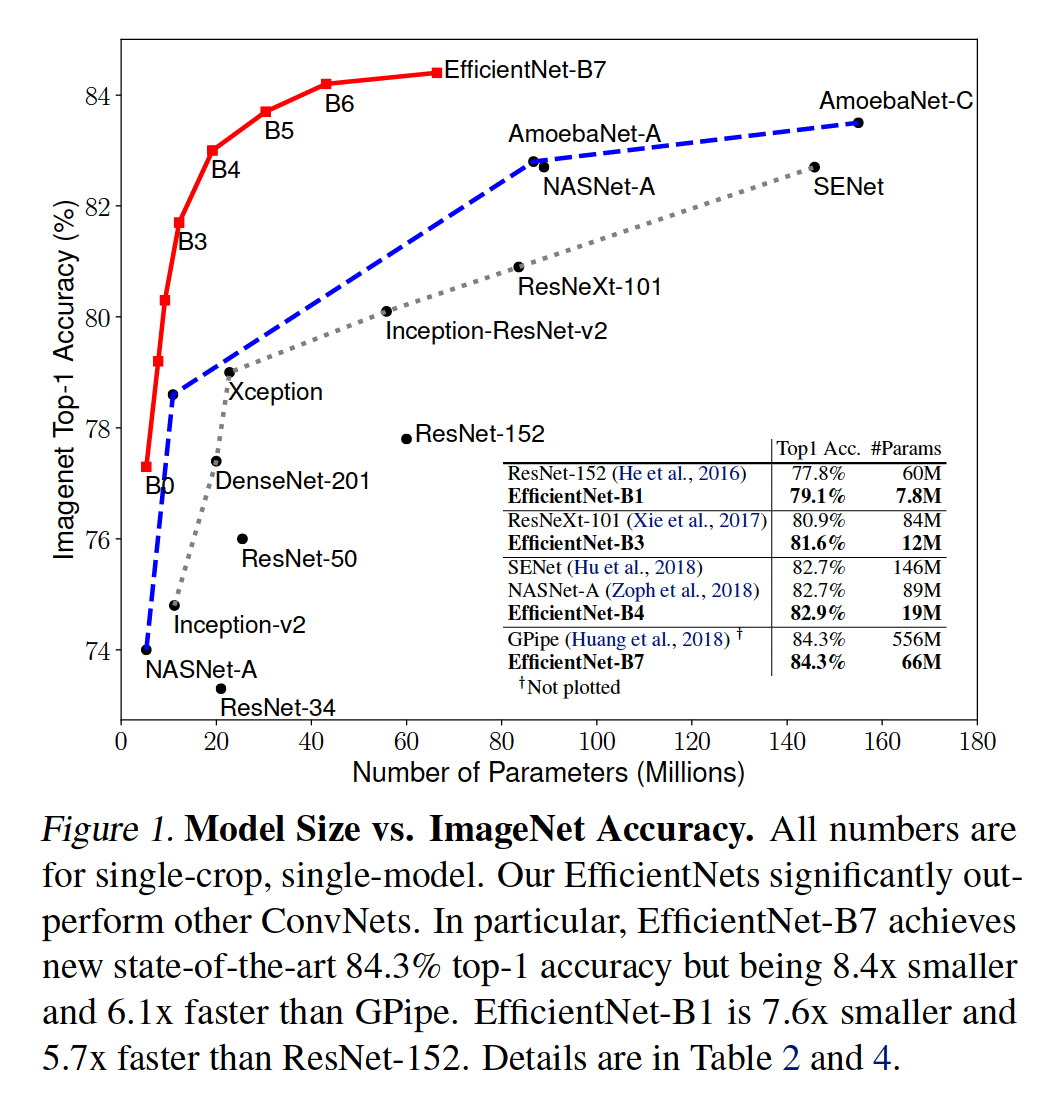
✔ EfficientNet-B0 ~ EfficientNet-B7 성능과 파라미터 개수, FLOPS
아래의 Table 2를 보면 확인할 수 있듯이 scaled EfficientNet은 top-1/top-5 accuracy가 기존의 모델들보다 월등할 뿐만 아니라, 파라미터 개수와 FLOPS도 감소시켰다는 점에서 혁신적이라고 할 수 있다. 특히 EfficientNet-B7은 GPipe보다 8.4배 적은 파라미터 개수 및 6.1배 빠른 결과를 보여주고 있다.
✔ 베이스라인을 MobileNet과 ResNet으로 하였을 때 Compound Scaling을 적용한 결과 성능과 FLOPS
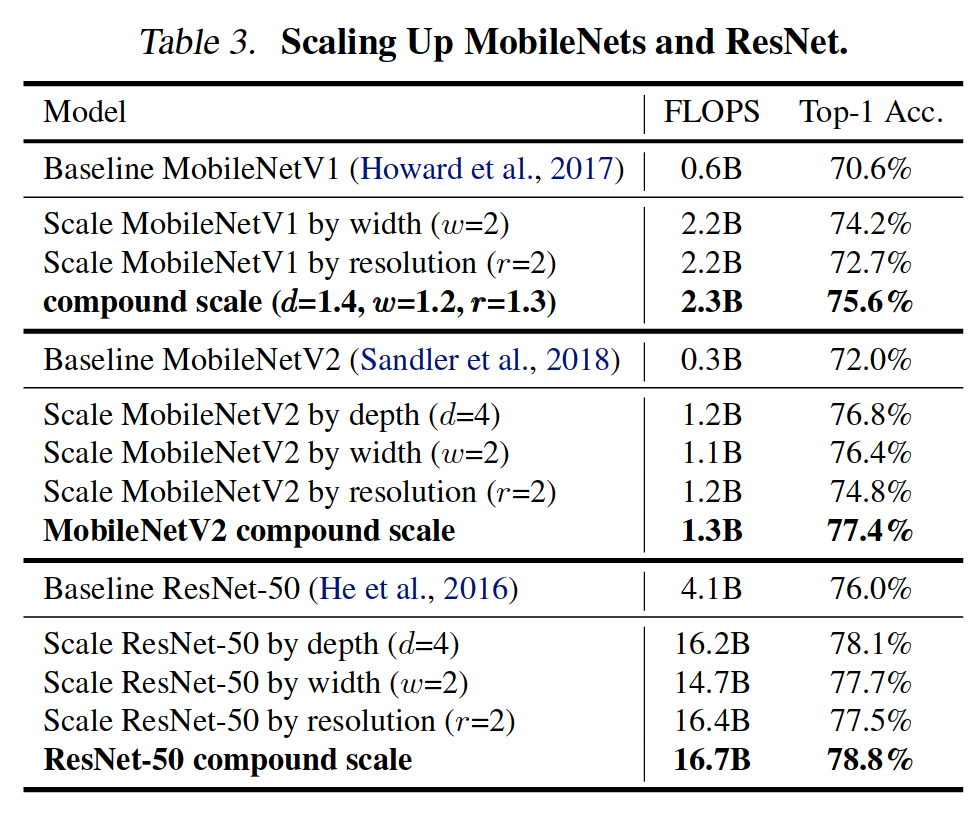
베이스라인을 EfficientNet-B0으로 하는 대신, 기존에 존재하는 MobileNet과 ResNet으로 하여 Compound Scaling을 적용하였을 때에도 그 성능과 효율성이 증대되었다는 결과를 확인 가능하다. 즉 Compound Scaling 기법은 EfficientNet뿐만 아니라 다른 모델로의 확장성이 좋다고 볼 수 있다.
✔ EfficientNet과 기존 모델과의 비교
EfficientNet은 기존 모델들보다 성능을 크게 향상시키고 파라미터 개수와 FLOPS를 줄였다는 점에서 그 이름대로 efficient하다.

'공부 > AI' 카테고리의 다른 글
| [DACON] LG 농업 환경 변화에 따른 작물 병해 진단 AI 경진대회 EDA 코드 (0) | 2023.04.07 |
|---|---|
| [Kaggle] PetFinder.my - Pawpularity Contest 후기 (Top 3%, Silver Medal) (0) | 2023.04.06 |
| [논문리뷰] Deep Residual Learning for Image Recognition (2015) (0) | 2023.01.31 |
| [논문리뷰] Going Deeper with Convolutions (2014) (0) | 2023.01.29 |
| [논문리뷰] Very Deep Convolutional Networks for Large-Scale Image Recognition (2014) (0) | 2023.01.28 |



